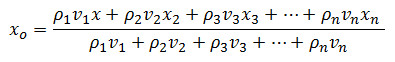NGOPREK QUIZ TITIK BERAT

Read More

NGOPREK QUIZ GERAK PARABOLA

Read More

NGOPREK QUIZ INDUKSI MAGNET

Read More

TITIK BERAT

Pernahkah Sobat Ngoprek melihat fenomena seperti video di bawah ini?

Menurut sobat mengapa hal tersebut bisa terjadi? Fenomena tersebut berkaitan dengan konsep titik berat. Apakah yang dimaksud dengan titik berat? Sobat Ngoprek bisa mempelajari penjelasan berikut.

Semua benda yang ada di permukaan bumi dipengaruhi oleh percepatan yang mengarah ke pusat bumi yang disebut gravitasi (disimbolkan g). Percepatan inilah yang menyebabkan benda bermassa mengalami gaya berat yang arahnya ke pusat bumi.

Gaya Berat (W) = m x g

Sebuah benda dapat sobat anggap tersusun atas partikel-partikel berukuran kecil yang mempunyai berat. Resultan dari berat partikel-partikel kecil itu membentuk resultan gaya berat yang mempunyai titik tangkap. Titik tangkap dari resultan gaya tersebut disebut titik berat benda. Dengan demikian dapat didefinisikan bahwa titik berat suatu benda merupakan titik tangkap resultan semua gaya berat yang bekerja pada setiap partikel penyusun benda tersebut.

Bagaimana Menetukan Titik Berat Suatu Benda?

 

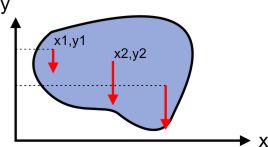
Coba sobat ngoprek perhatikakan gambar di bawah di atas. Misalkan ada sebuah benda tegar yang sobat bagi-bagi menjadi beberapa bagian-bagian yang lebih kecil. Bagian-bagian tersebut kemudian kita sebut dengan partikel. Jika kita namakan partikel tersebut partikel 1,2,3,…, n dan masing-masing memiliki berat W₁, W₂, W₃, …, Wn dan masing-masing memiliki titik tangkap gaya berat di (x₁,y₁),(x₂,y₂),(x₃,y₃),….,(x_n,y_n). Setiap partikel akan menghasilkan suatu momen gaya terhadap titik asal koordinat yang besarnya sama dengan perkalian gaya berat (massa x g) dikali dengan lengan momennya (x).

τ1 = W₁ . x₁
τ2 = W₂ . x₂
τ3 = W₃ . x₃
τn = W_n . x_n

Sekarang kita akan coba menentukan koordinat gaya berat (W) yang akan menghasilkan efek yang sama dengan semua pada semua partikel-partikel yang menyusunnya. Dari momen gaya total yang dihasilkan oleh W yang bekerja pada titik berat (misal x_o) dirumuskan

τo = W. xo = W₁ . x₁ +  W₂ . x₂ + W₃ . x₃ + … + W_n . x_n

karena W =  W₁+ W₂+ W₃+ … + Wn maka didapat rumus titik berat benda

 

seandainya benda dan sumbu-sumbu pembandinganya (sumbu x dan sumbu y) diputar 90 derajat maka gaya gravitasi akan berputar 90 derajat pula. Tidak ada perubahan sedikitpun pada berat total benda. Tetapi besarnya momen gaya dari tiap partikel akan berubah karena lengan momennya bukan lagi jark x dari titik pusat melainkn jarak y dari titik pusat. Jika titik berat benda pada sumbu y adalah y_o maka cara menentukan posisi y_o bisa menggunakan rumus

  

Dari kedua rumus di atas, sobat bisa perhatikan kalau dari rumus
W = m.g sehingga
W₁ = m₁.g₁, W₂ = m₂.g₂, dan seterusnya dengan demikian variable g dapat kita coret sehingga kita bisa mencari titik berat benda dari massa partikel dengan menggunakan rumus

 

Keterangan Rumus
x_o = absis (x) dari titik berat benda
y_o = ordinat (y) dari titik berat benda
m_i = massa partikel ke-i
x_i = absis titik tangkap dari partikel ke-i
y_i = ordinat titik tangkap dari partikel ke-i

Untuk memudahkan sobat mencari titik berat dari luas benda (dimensi dua) berikut tabel rumusnya.

Titik Berat Benda Homogen Berdimensi Tiga

Ada hubungan antar massa dan volume m = ρV dengan ρ adalah massa jenis benda. Dengan demikian untuk setiap partikel m1 = ρ1 . v1, m2 = ρ2 . v2, dan seterusnya, sehingga absis dari titik berat benda dapat dihitung dengan rumus

karena ρ (rho) benda sama, maka bisa dicoret, menghasilkan persamaan:

Untuk memudahkan sobat mencari titik berat dari benda ruang (dimensi tiga) berikut tabel rumusnya.

Untuk menambah pemahamanmu, jawablah pertanyaan berikut.

 

Lakukan percobaan berikut.

 

Read More

NGOPREK SOAL TITIK BERAT

Soal No. 1

Tentukan koordinat titik berat susunan enam buah kawat tipis berikut ini dengan acuan titik 0 !





Pembahasan
Data dari soal :
l₁ = 20, X₁ = 20, Y₁ = 10
l₂ = 20, X₂ = 60, Y₂ = 10
l₃ = 80, X₃ = 40, Y₃ = 20
l₄ = 20, X₄ = 0, Y₄ = 30
l₅ = 40, X₅ = 40, Y₅ = 40
l₆ = 20, X₆ = 80, Y₆ = 30

Koordinat titik berat gabungan keenam kawat (X₀ , Y₀)

Soal No.2

Tentukan letak titik berat bangun berupa luasan berikut dihitung dari bidang alasnya!



Pembahasan

Data dari soal :
Benda 1 (warna hitam)
A₁ = (20 x 60) = 1200
Y₁ = 30
Benda 2 (warna biru)
A₂ = (20 x 60) = 1200
Y₂ = (60 + 10) = 70

Soal No.3 

Tentukan letak titik berat bangun berikut terhadap alasnya!



Pembahasan

Bagi bangun menjadi dua, persegi di bagian bawah dan segitiga sama kaki di bagian atas. Data :
Bidang 1 (persegi)
A₁ = (90 x 90) = 8100
Y₁ = 90/2 = 45
Bidang 2 (segitiga)
A₂ = 1/2(90 x 90) = 4050
Y₂ = 1/3(90) + 90 = 120

Letak Y_o :

Soal No.4

Tentukan letak titik berat bangun berikut terhadap alasnya!



Pembahasan

Bagi bidang menjadi dua, persegi panjang yang dianggap utuh (belum dilubang) dan lubang berbentuk segitiga. Data dari soal :
Bidang 1 (Persegi panjang utuh)
A₁ = (180 x 90) = 16200
Y₁ = (180/2) = 90
Bidang 2 (lubang segitiga)
A₂ = 1/2(90 x 90) = 4050
Y₂ = 180 − (90/3) = 150

Letak Y_o :

Soal No.5

Sebuah tabung pejal disambung dengan kerucut pejal seperti pada gambar berikut!



Tentukan letak titik berat bangun tersebut terhadap garis AB!

Pembahasan

Data :
Bangun 1 (Tabung pejal)
V₁ = π r² t = 12π r²
X₁ = 6
Bangun 2 (Kerucut pejal)
V₂ = 1/3 π r² t = 4 π r²
X₂ = 12 + (1/4 t) = 12 + 3 = 15

Letak X_o :

Soal No.6

Karton I dan II masing-masing homogen , terbuat dari bahan yang sama dan digabung menjadi satu seperti gambar di bawah.

Tentukan koordinat titik berat benda gabungan dari titik A
(Soal Ebtanas Fisika 1988 - Essay)

Pembahasan
Karton 1
A₁ = 4 x 8 = 32
x₁ = 4
y₁ = 2

Karton 2
A₂ = 4 x 4 = 16
x₂ = 8 + 2 = 10
y₂ = 4 + 2 = 6

Titik berat benda gabungan dengan demikian adalah


Letak titik berat dari titik A adalah 6 cm ke kanan dan 3,3 cm ke atas.

Soal No.7

Benda 1 dan benda 2 berupa luasan disusun seperti gambar berikut ini.

Tentukan jarak titik berat benda 1 dan benda 2

Pembahasan
Letak titik berat benda 1 diukur dari alas benda 1 adalah y₁ = ^d/₂ = 0,5 d
Letak titik berat benda 2 diukur dari alas benda 1 adalah y₂ = d + ¹/₃(3d) = d + d = 2d

Sehingga jarak kedua titik adalah:
2d − 0,5 d= 1,5 d

Soal No.8

Diberikan sebuah bangun datar sebagai berikut.

Tentukan koordinat titik berat diukur dari titik O.

Pembahasan
Bagi luasan menjadi dua, tentukan titik berat masing-masing luasan seperti ini.

A₁ = = 12 x 12 = 144
x₁ = 6
y₁ = 6

A₂ = 1/2 x 12 x 12 = 72
x₂ = 12 + 4 = 16
y₂ = 4

Sehingga



Koordinat titik berat dari titik O adalah (9,33 , 5,33)

Soal No.9

Tentukan lokasi titik berat luasan berikut ini diukur dari sumbu x!

Pembahasan
Bagi luasan menjadi 3 bagian. Diukur terhadap sumbu x artinya y_o yang dicari.

Data yang diperlukan:
A₁ = 20 x 50 = 1000
y₁ = 25

A₂ = 30 x 20 = 600
y₂ = 40

A₃ = 20 x 10 = 200
y₃ = 15

 

 

Soal No.10

Sebuah kubus dengan panjang sisi 2 meter ditempatkan di bawah sebuah balok dengan ukuran seperti gambar.



Tentukan letak titik berat gabungan kedua benda diukur dari alas kubus!

Pembahasan
Volum Kubus dan ordinat (y) kubus:
V₁ = 2 x 2 x 2 = 6 V₁ = 2 x 2 x 2 = 8
y₁ = 2/2 = 1

Volum Balok dan ordinat (y) balok:
V₂ = 2 x 1,5 x 1 = 3
y₂ = 2 + 1 = 3

Letak Yo dari alas kubus

Read More

NGOPREK SOAL GERAK PARABOLA

Soal No. 1

Perhatikan gambar berikut ini! Sebuah peluru ditembakkan dengan kelajuan awal 100 m/s dan sudut elevasi 37^o . Jika percepatan gravitasi bumi 10 m/s², sin 37^o = 3/5 dan cos 37^o = 4/5
Tentukan:



a) Penguraian vektor kecepatan awal terhadap arah horizontal (sumbu X)
b) Penguraian vektor kecepatan awal terhadap arah vertikal (sumbu Y)
c) Kecepatan peluru saat t = 1 sekon
d) Arah kecepatan peluru saat t = 1 sekon terhadap garis mendatar (horisontal)
e) Tinggi peluru saat t = 1 sekon
f) Jarak mendatar peluru saat t = 1 sekon
g) Waktu yang diperlukan peluru untuk mencapai titik tertinggi
h) Kecepatan peluru saat mencapai titik tertinggi
i) Tinggi maksimum yang bisa dicapai peluru ( Y_maks )
j) Waktu yang diperlukan peluru untuk mencapai sasaran (jarak terjauh arah mendatar)
k) Jarak terjauh yang dicapai peluru ( X_maks )
Jawab
a) Penguraian vektor kecepatan awal terhadap arah horizontal (sumbu X)

b) Penguraian vektor kecepatan awal terhadap arah vertikal (sumbu Y)

c) Kecepatan peluru saat t = 1 sekon
Karena gerak parabola terbentuk dari dua buah jenis gerak, yaitu GLBB pada sumbu Y dan GLB pada sumbu X, maka terlebih dahulu harus dicari kecepatan gerak peluru saat 1 sekon untuk masing-masing sumbu.
Pada sumbu X :
Karena jenis geraknya GLB (gerak lurus beraturan) maka kecepatannya selalu konstan , jadi akan sama dengan kecepatan awal untuk sumbu X jadi :

sumbu Y:
Jenis gerakan pada sumbu Y adalah GLBB jadi ingat rumus untuk mencari kecepatan saat t yaitu V_t = V_o - gt dengan V_o disini diganti V_o miliknya Y atau V_oy

kecepatan " saja

d) Arah kecepatan peluru saat t = 1 sekon terhadap garis mendatar (horisontal)
Arah kecepatan bisa diwakili oleh nilai sinus, cosinus atau tan dari suatu sudut, kalo mau sudutnya tinggal ubah saja jika sudah diketahui nilai sin, cos tan nya. Disini kita pakai nilai tan sudut katakanlah namanya sudut Θ dimana:

Besar sudutnya..., cari pakai kalkulator karena bukan sudut istimewa.
e) Tinggi peluru saat t = 1 sekon
Saat 1 sekon ketinggian peluru namakan saja Y atau h juga boleh,...

f) Jarak mendatar peluru saat t = 1 sekon
Saat 1 sekon jarak mendatar peluru namakan saja X

g) Waktu yang diperlukan peluru untuk mencapai titik tertinggi
Titik tertinggi dicapai peluru saat kecepatan pada sumbu Y adalah NOL. Sehingga:

h) Kecepatan peluru saat mencapai titik tertinggi
Karena saat titik tertinggi V_ty = 0, maka tinggal V_tx saja yang ada nilainya sehingga:
V_t = V_tx = Vo cos α = 100(4/5) = 80 m/s
i) Tinggi maksimum yang bisa dicapai peluru
Tinggi maksimum namakan Y _maks atau di soal biasanya h_max,..tinggal pilih saja :

j) Waktu yang diperlukan peluru untuk mencapai sasaran (jarak terjauh arah mendatar)
Waktu untuk mencapai jarak mendatar paling jauh adalah dua kali waktu untuk mencapai ketinggian maksimum sehingga hasilnya 2 x 6 = 12 sekon.
k) Jarak terjauh yang dicapai peluru
Cara pertama, dipakai jika sudah diketahui waktunya (12 sekon)
Xmaks = (Vo cos α ) t = 100(4/5)12 = 960 meter
Cara kedua anggap saja belum diketahui waktunya :

Soal No.2

Sebuah peluru ditembakkan dari moncong sebuah meriam dengan kelajuan 50 m/s arah mendatar dari atas sebuah bukit, ilustrasi seperti gambar berikut.



Jika percepatan gravitasi bumi adalah 10 m/s² dan ketinggian bukit 100 m
Tentukan :
a. Waktu yang diperlukan peluru untuk mencapai tanah
b. Jarak mendatar yang dicapai peluru (S)
Jawab
a) Waktu yang diperlukan peluru untuk mencapai tanah
Tinjau gerakan sumbu Y, yang merupakan gerak jatuh bebas. Sehingga V_oy = O dan ketinggian bukit namakan Y (di soal dinamakan h)
Y = 1/2 g t²
100 = (1/2)(10) t²
t = √20 = 2√5 sekon
b) Jarak mendatar yang dicapai peluru (S)
Jarak mendatar gerakan berupa GLB karena sudutnya nol terhadap horizontal langsung saja pakai rumus:
S = V t
S = (50)( 2 √5) = 100 √5 meter

Soal No.3

Sebuah bola dilontarkan dari atap sebuah gedung yang tingginya adalah h = 10 m dengan kelajuan awal V₀ = 10 m/s

Jika percepatan gravitasi bumi adalah 10 ms² , sudut yang terbentuk antara arah lemparan bola dengan arah horizontal adalah 30^o dan gesekan bola dengan udara diabaikan,,
Tentukan :
a) Waktu yang diperlukan bola untuk menyentuh tanah
b) Jarak mendatar yang dicapai bola
Jawab
a) Waktu yang diperlukan bola untuk menyentuh tanah ketinggian gedung h atau sama dengan Y disini :

ambil nilai positif sehingga t = 2 sekon
Catatan : Jangan lupa tanda minus pada nilai Y, karena kalau plus berarti 10 meter diatas tempat pelemparan, sementara posisi yang dicari adalah 10 meter dibawah tempat pelemparan.
b) Jarak mendatar yang dicapai bola
 
  

Soal No.4

Sebuah peluru ditembakkan dengan kecepatan 60 m/s dan sudut elevasi 30°. Ketinggian maksimum yang dicapai adalah....
A. 30 m
B. 45 m
C. 50 m
D. 90 m
E. 100 m
(Sumber soal UMPTN 1997)

Jawab
Data dari soal:
v_o = 60 m/s
α = 30°
Y_maks = ......

                v_o ² sin² α
Y_maks = ^{_______________________}
                         2g

                  (60) ² (sin 30° )²
Y_maks = ^{_______________________}
                        2(10)

                       (60) ² (1/2 )²
Y_maks = ^{_______________________} = 45 meter
                           20

Soal No.5

Peluru ditembakkan condong ke atas dengan kecepatan awal v = 1,4 x 10³ m/s dan mengenai sasaran yang jarak mendatarnya sejauh 2 x 10⁵ m. Bila percepatan gravitasi 9,8 m/s², maka elevasinya adalah n derajad, dengan n sebesar....
A. 10
B. 30
C. 45
D. 60
E. 75
(Sumber soal UMPTN 1993)

Jawab
Data dari soal:
v_o = 1,4 x 10³ m/s
Xmaks = 2 x 10⁵ m
α = .......

Dari rumus jarak mendatar maksimum:

                      v_o ² sin 2 α
X_maks = ^{_________________}
                             g
                       (1,4 x 10³) ² sin 2 α
2 x 10⁵ = ^{_________________________}
                                  9,8

                                 2 x 10⁵ x 9,8
sin 2 α = ^{______________________________}
                           (1,4 x 10³) ²

sin 2 α = 1
sin 2α = sin 90°
α = 90°/₂ = 45 °

Read More